Applikationsschrift 142

Die Modellierung zusätzlicher Strukturen mit Si6000b

Was ist zu tun, wenn die gewünschte impedanzkontrollierte Struktur nicht in der Polar Si6000b enthalten ist ? - zwei Tricks, die Ihnen helfen, die Berechnung dennoch durchzuführen:

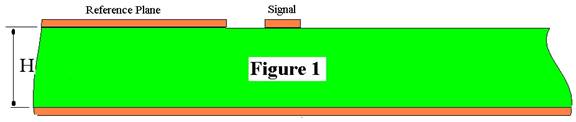
Wie viele Strukturen von der Si6000b auch unterstützt werden (derzeit 39) - es werden nie genug sein, um alle Spezialanwendungen abzudecken. Wenn Si6000b die gewünschte Struktur nicht enthält,  so können Ihnen die folgenden Tricks helfen, das Problem zu umgehen und dennoch genaue Impedanzwerte zu berechnen.

1. Erhöhen Sie die Strukturabmessungen

Ein Beispiel für diese Technik ist die Modellierung einer koplanaren Struktur, welche nur eine Massefläche an einer Seite der Leiterbahn aufweist (und nicht beidseits, wie bei koplanaren Strukturen ansonsten üblich). Diese semi-koplanare Struktur (auch als uniplanar bezeichnet) wird in bestimmten Anwendungen z.B. in der Konsumerelektronik eingesetzt.

Eine semi-koplanare Struktur kann wie in Abbildung 1 aussehen:

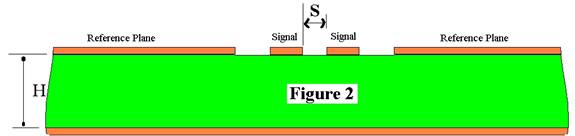
Abbildung 1

Die Si6000b enthält keine Struktur welcher exakt der Abgebildeten entspricht. Si6000b bietet jedoch eine Differential Surface Coplanar Waveguide Struktur wie in Abbildung 2:

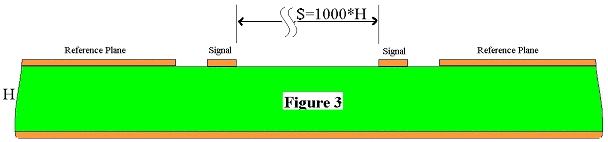
Abbildung 2

Durch Erhöhen des Abstandes S zwischen den differentiellen Signalleitern auf einen sehr hohen Wert, bis sich die Impedanz nicht mehr weiter erhöht, können wir die Struktur in Abbildung 1 emulieren. Erhöhen der Wertes S auf 1000 x H, der Dicke des Dielektrikums reicht dazu völlig aus. Dieser Fall wird in Abbildung 3 gezeigt.

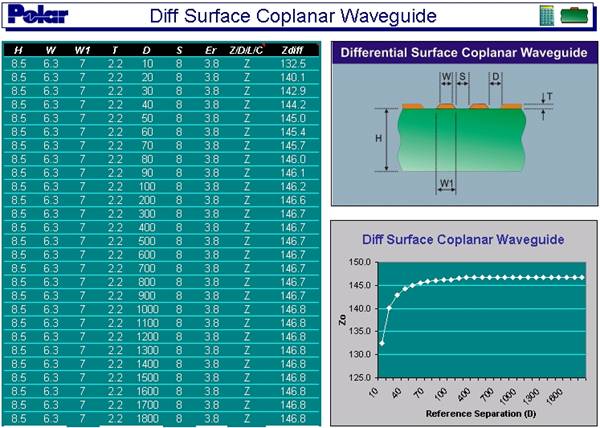
Abbildung 3

Bei diesem großen Abstand sind die beiden differentiellen Leitungen nicht mehr länger gekoppelt, aber der Si6000b Field Solver ist dennoch in der Lage, die differentielle Impedanz Zo(diff) der Struktur genau zu berechnen. Wir erinnern uns, dass die differentielle Impedanz Zo(diff) des differentiellen Leitungspaars dem zweifachen Wert von Zo(odd), der charakteristischen Impedanz einer einzelnen unsymmetrischen Leitung entspricht. Ein Beispiel für diese Berechnung mittels der Si6000b wird in Abbildung 4 gezeigt.

Abbildung 4

Zo(diff) ergibt einen Wert von 244 Ohm. Geteilt durch zwei ergibt sich daher ein Wert von 122 Ohm für die semi-koplanare Struktur.

Ein weiteres Beispiel für die Verwendung großer Abstände zum Ausblenden unerwünschter Komponenten ist die Berechnung der differentiellen Impedanz eines Leitungspaars ohne Bezugslage. Obwohl diese Struktur theoretisch nicht optimal ist, so wird sie doch in der Praxis zur Kosteneinsparung eingesetzt. Um diese Struktur zu modellieren, verwenden wir die Si6000b Differential Coplanar Waveguide Struktur und erhöhen den Abstand zur Bezugsfläche so weit, bis keine weitere Erhöhung der Impedanz eintritt. Wir illustrieren den Effekt mittels einem Si6000b Excel-Tabellenblatt in Abbildung 5:

Abbildung 5

Beachten Sie, wie die Erhöhung von D auf  200 mils (die 100-fache Kupferstärke in dieser Struktur) zu keiner weiteren Erhöhung der Impedanz führt. Die Impedanz des Signalpaares ohne Bezugsfläche beträgt 147 Ohm bei den gegebenen Abmessungen.

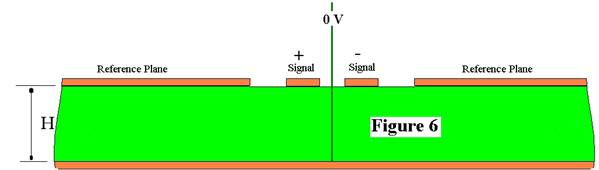
2. Setzen Sie virtuelle Masseflächen ein

Es ist uns oft nicht bewusst, dass eine virtuelle Bezugsmasse zwischen einem differentiellen Leiterpaar (im Odd-Mode-Betrieb) besteht. Betrachten wir die Leiter in Abbildung 6 im differentiellen Betrieb.

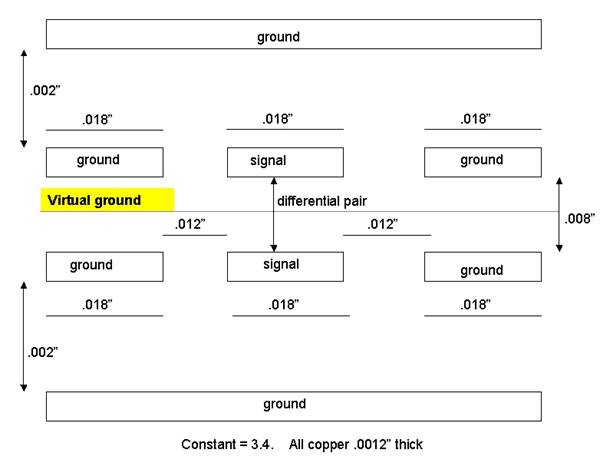
Abbildung 6

Da die Leiter mit gleichen Signalen, jedoch gegenpolig beaufschlagt werden, ist das elektrische Feld bei jedem äquidistanten Punkt zwischen den Leitern 0 V (in der Mitte zwischen +V und -V). Wir können dies zu unserem Vorteil nutzen, um manche Berechnungen zu vereinfachen oder spezielle Strukturen zu berechnen. Betrachten wir die kundenspezifische Struktur in Abbildung 7 unten:

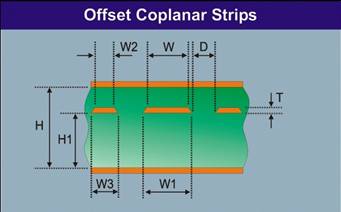
Abbildung 7

Die Si6000b enthält keine entsprechende Struktur, jedoch eine Offset Coplanar Strips Struktur wie in Abbildung 8 unten:

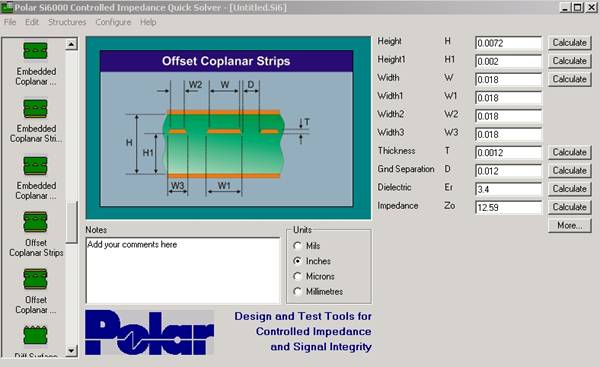
Abbildung 8

Er ist einfach erkennbar, dass diese Struktur die Hälfte der Struktur in Abbildung 7 darstellt. Die untere Lage entspricht der unteren Masselage in Abbildung 7. Die Signal- und Masseleitungen in Abbildung 8 entsprechen den unteren signal- und Masseleitungen in Abbildung 7. Die obere Masselage in Abbildung 8 entspricht der virtuellen Massefläche in Abbildung 7. Eine ähnliche Übereinstimmung gilt für die obere Hälfte in Abbildung 7. Für unsere Betrachtungen nehmen wir an, dass in Abbildung 8 nur eine Leitung mit der Spannung V beaufschlagt wird. In Abbildung 7 werden beide Signalleitungen angesteuert, eine mit +V und eine mit -V. In Abbildung 7 ist daher die Signalspannung doppelt so hoch wie in Abbildung 8 (= + V -(-V) = 2V), der Strom ist jedoch gleich. Daher ist die Impedanz in Abbildung 7 doppelt so hoch wie in Abbildung 8. Wir verwenden Abbildung 8 um die Impedanz Zo(odd) für eine der beiden differentiellen Leitungen in Abbildung 7 zu bestimmen. Daraus ergibt sich die differentielle Impedanz Zo(diff) für das Leitungspaar durch die Beziehung Zo(diff) = 2*Zo(odd). Der Si6000b Quick Solver dient zur einfachen Berechnung der Impedanz wie in Abbildung 9.

Abbildung 9

Der Wert für Zo(odd) beträgt 12,59 Ohm, daher ergibt sich eine differentielle Impedanz Zo(diff) für die zusammengesetzte Struktur in Abbildung 7 als 2*12.59 = 25,18 Ohm.

Schlußfolgerung:

Die Strukturen in Si6000b sind Werkzeuge. Betrachten Sie diese Werkzeuge über Ihre ursprüngliche Funktion hinaus, um zu prüfen, ob diese für Ihre speziellen Anforderungen adaptiert werden können. Besonders hilfreiche Techniken sind die Erhöhung von Abständen zum Ausblenden der Auswirkungen von ungewünschten Strukturelementen und der Einsatz von virtuellen Masseflächen zwischen differentiellen Leiterpaaren, um eine unsymmetrische Struktur zu modellieren.

Beachten Sie auch, wie die Excel-Tabellen und die Grafiken dazu verwendet werden, um den Einfluss der Abmessungen zu untersuchen. Die Flexibilität des Quick Solvers erlaubt es, Maßangaben in gemischten Einheiten einzugeben. So können z.B. für eine einzelne Berechnung die Parameter gemischt in Mils und Micron eingegeben werden.