|
|
|
The Effect of Etch Taper, Prepreg and Resin Flow on the Value of Differential Impedance
Presented at IPC Expo 2002
by
Alan Staniforth and Martyn Gaudion
Introduction
Many printed circuit board manufacturers report that the measured value of the differential impedance is a few ohms greater than the calculated value when the substrate is FR4. There maybe several reasons for these differences:
- accuracy of the software used
- accurate knowledge of the track cross-section
- the variation of the dielectric constant of the substrate
Accuracy of the software
The software used by the authors1 agrees, where possible, with good accurate theoretical impedance equations, particularly when the track thickness is zero. In addition, the new software referred to in Section 3, gives values of impedance which are within 25x10-2% of the values calculated by the software of Reference 1. Thus it is concluded that the calculated impedances are accurate.
Accuracy of the track cross-section
In the calculations the cross-section of the track is assumed to be a regular trapezium, i.e. there are equal etch tapers at each side of the track. Figure 1 shows an embedded pair of identical microstrip tracks. To reduce computation memory and time most commercial software assumes symmetry about the centreline shown in Figure 1, to calculate the differential impedance. This means that the etch taper is the same for both tracks.
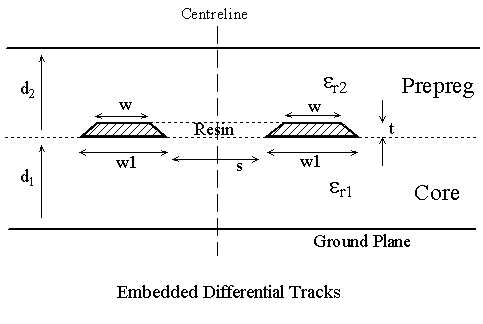
Fig 1
Table 1 shows the differential impedance for embedded microstrip track with different etch tapers.
w(µm) |
Etch taper each side (µm) |
Differential Impedance Zdiff (ohms) |
75 65 55 |
0 5 10 |
99.2565 102.293 104.998 |
Table 1
w1 = 75, d1 = 500, d2 = 100, s = 100, t = 35. All dimensions in µm.
e r1 = e r2 = 4.2
Table 1 shows that the impedance can vary by several ohms depending on the amount of taper. Thus in order to calculate the impedance accurately the amount of etch taper must be known.
Prepreg and resin flow
During the manufacture of embedded microstrip and stripline, the track is etched on core FR4, and then prepreg FR4 added by pressure and heat above the track. Prepreg has less fibreglass and more resin than core material. During the manufacture of differential tracks resin can flow into the space between the tracks as shown in Figures 1 and 2.
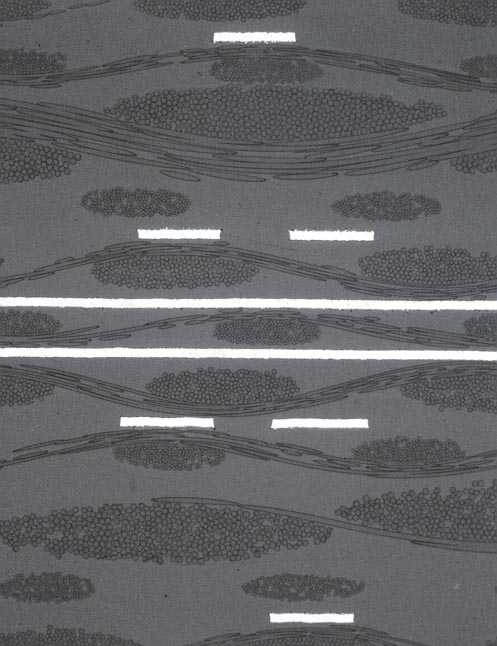
Fig 2: Photo of resin flow
Variation of the dielectric constant
The dielectric constant of prepreg is less than core material because the average dielectric constant depends on the proportions of glass fibre and resin [2]. The dielectric constant of glass fibre is 6.1 and resin is approximately 3.2. Because most software available for calculating the impedance of tracks assumes that the dielectric constant of both the core and prepreg is the same, an average value, 4.2, is used for both core and prepreg. This can lead to discrepancies between calculated and measured impedance values, especially if resin flows into gaps.
Software has been developed to calculate the impedance when the substrate has layers of different materials. It can also be adapted for a thin layer of resin between the tracks. This software uses a different method from that used in Reference 1. The results of calculations for the impedance of differential embedded microstrip, and stripline, are described in the next section.
Calculations
Table 2 summarises the differential impedance results for embedded microstrip.
Core e r1 |
Prepreg e r2 |
Resin (see Fig 1) e resin |
Differential Impedance Zdiff (ohms) |
|
A |
B |
|||
4.2 |
4.2 3.8 3.8 3.8 |
3.8 3.2 |
102.29 104.87 104.86 106.53 |
103.23 105.79 105.78 106.88 |
4.5 |
3.9 3.9 3.9 |
3.9 3.2 |
102.54 102.52 104.36 |
103.35 103.34 104.55 |
Table 2
w1 = 75, w = 65, d1 = 500, d2 = 100.
Column A: s = 100, t = 35
Column B: s = 75, t = 17
All dimensions in µm.
Table 3 shows the results for stripline.
Core e r1 |
Prepreg e r2 |
Resin (see fig 1) e resin |
Differential Impedance Zdiff (ohms) |
|
A |
B |
|||
4.2 |
4.2 3.8 3.8 3.8 |
3.8 3.2 |
74.114 76.469 76.467 77.343 |
96.825 99.752 99.732 101.188 |
4.5 |
3.9 3.9 3.9 |
3.9 3.2 |
74.849 74.848 75.811 |
97.576 97.557 99.154 |
Table 3
w1 = 75, w = 65, s = 100, t = 35.
Column A: d1 = d2 = 100,
Column B: d1 = d2 = 500
All dimensions in µm.
For both tables, the basic impedance computed is shown for an assumed homogenous material with a dielectric constant e r of 4.2; the assumption for this control calculation is that the e r between the tracks is the same as the dielectric constant of the bulk material. If we assume the prepreg layer is resin rich compared to the core, introducing a layer of e r 3.8 above the core material increases the impedance by 2.5 to 3.0 ohms. As a control we now introduce a 3rd dielectric, that of the resin, between the traces. First as a control the resin value is set equal to the prepreg, and as expected the field solver outputs an almost identical result. The next step is to test the effect of a pure resin area between the two traces, and in this case the e r between the traces is further reduced to 3.2. With this additional section of resin the impedance increases by a further 1.0 to 1.5 ohms.
This result contrasts how the simplistic assumption that and FR4 stack up has a homogenous e r of 4.2 can contribute to variation between predicted and finished impedance, and, how the effect is further magnified when the effect of resin rich areas between differential or coplanar structures is taken into account.
In addition to the effects of resin rich areas, Table 1 also describes how etch taper can further influence the variation between predicted and measured results. As this taper also tends to enlarge the resin rich area it can be seen that both the taper and the resin rich area can contribute to the uncertainty of predictions. A sound knowledge of finished geometry through micro-sectioning of individual production samples is the preferred way to minimise these variations. Table 1 shows how etch taper variation of between 0 and 10 µm can contribute over 5 ohms of variation between predicted and measured impedance.
Measurement equipment will also have its own tolerance and sources which contribute to variation; the study of these is outside the scope of this paper.
Conclusions
Based on the differential impedance calculated assuming that the dielectric constant of both FR4 core and prepreg is 4.2, the calculations show that a flow of resin between differential tracks during manufacture, can increase the impedance for embedded microstrip by between 3.5 and 4.0 ohms, and for stripline by between 3.0 and 3.5 ohms.
However the calculations show that a difference in the dielectric constant of the core and the prepreg is important. In practice these constants will be different because of the different proportions of glass fibre and resin.
The calculations also show that a knowledge of the actual etch taper is also important.
References
- Si8000m software, Polar Instruments.
- Alan Staniforth, Gary Rich, Chris Gregg, Calculation of the Differential Impedance of Tracks on FR4 Substrates. Proceedings IPC Conference, April 2000, pp S11-1-1 to S11-1-5.